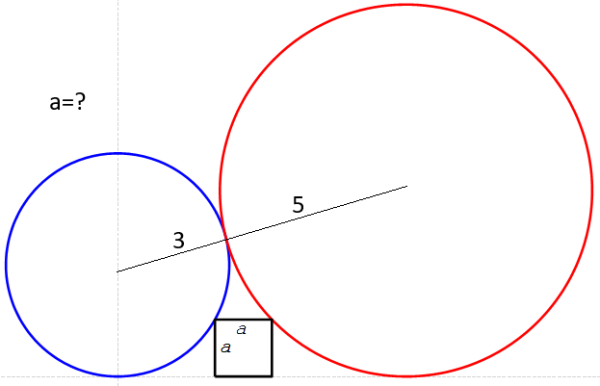
Эту https://www.anekdot.ru/id/1549126 вирусную задачу каждый ... решит. А ты попробуй решить вот это!
Мем №1550122
Эту https://www.anekdot.ru/id/1549126 вирусную задачу каждый ... решит. А ты попробуй решить вот это!
+-40–
Выпуск: мемы 03 октября 2025
Проголосовало за – 25, против – 65
Статистика голосований по странам
Статистика голосований пользователей
Чтобы оставить комментарии, необходимо авторизоваться. За оскорбления и спам - бан.
22 комментария, показывать
сначала новые
сначала новыесначала старыесначала лучшиеновые - список
Короче, решение для ленивых. Копируешь фото, вставляешь в Google с "решить задачу". Опа, ответ: √28. Интересно, а такой способ решения легитимен? Если нужно быстро решить задачу и неважно как ты нашёл ответ?
+0–
ответить
ИИ облажался. А если серьёзно, назовите конкретную ситуацию, когда подобные исчисления необходимы.
+0–
ответить
>А если серьёзно, назовите конкретную ситуацию, когда подобные исчисления необходимы.
Её обозначил Ю.
Придут к тебе два товарища с фамилиями Паркинсон и Альцгеймер и спросят: "Третьим будешь?". А ты решишь при них подобную задачу и они уйдут ни с чем!
+0–
ответить
А вы смотрели фильмы "Доказательство" и "Игры разума"? Главные герои тоже решали интересные задачи. И к ним пришли ребята покрепче чем Паркинсон с Альцгеймером. А вообще в математике полно простых логических ошибок, которые никто исправлять не собирается. Математика не панацея.
+0–
ответить
А оно мне надо? В пятницу, на 63-м году жизни на развлекательном сайте решать задачи?
Кто-то из нас двоих слегка ебобо. Надеюсь, не я.
+3–
ответить
\\\на 63-м году жизни \\\
Решение сложных и новых задач в преклонном возрасте отсрочивает наступление когнитивных нарушений и деменции - это любой врач скажет ) И день недели и локация никакой роли не играют.
+1–
ответить
Начало Ю указал, это в любом случае первый шаг. Потом бы я решал не геометрией, а алгеброй - системой 4 уравнений 2 окружностей, горизонтальной и вертикальной прямой (сторон квадрата)
Хотя, можно и геометрически.
В начале координат рисуем радиусом 3, потом пунктиром радиусом 8, строим и горизонталь 2 (разница радиусов). В точке пересечения окружность радиусом 5
Дальше нужно знать геометрию, или поверить на слово )))
Строим биссектрису угла между линией радиусов и осью ОХ, потом нормаль к "линии радиусов" из точки пересечения окружностей, находим точку пересечения этой нормали с осью ОХ (проекция отрезка между центрами). А в финале строим нормаль к биссектрисе так, чтоб она проходила через предыдущую точку.
Это нормаль пройдет точно через центр искомого квадрата со сторонами примерно 1,53. Разумеется угол между нормалями будет равен половине угла между центрами окружностей и горизонталью
Есть и более изящный способ, метод хорд (горизонтали из 2 полухорд и искомой стороны квадрата, а хорда определяется до радиусу и второй стороне квадрата).
Хотя, конечно, системой уравнений решать логичнее
+0–
ответить
Не, для школьников пожалуй метод хорд в лоб будет сложно, там корни им будет тяжело найти
sqrt(6a-a^2) + sqrt(10a-a^2) + a = 2sqrt(15)
+1–
ответить
Для школьников - это раз плюнуть.
Ответ правильный, но есть более понятный метод через решения системы квадратных уравнений.
+0–
ответить
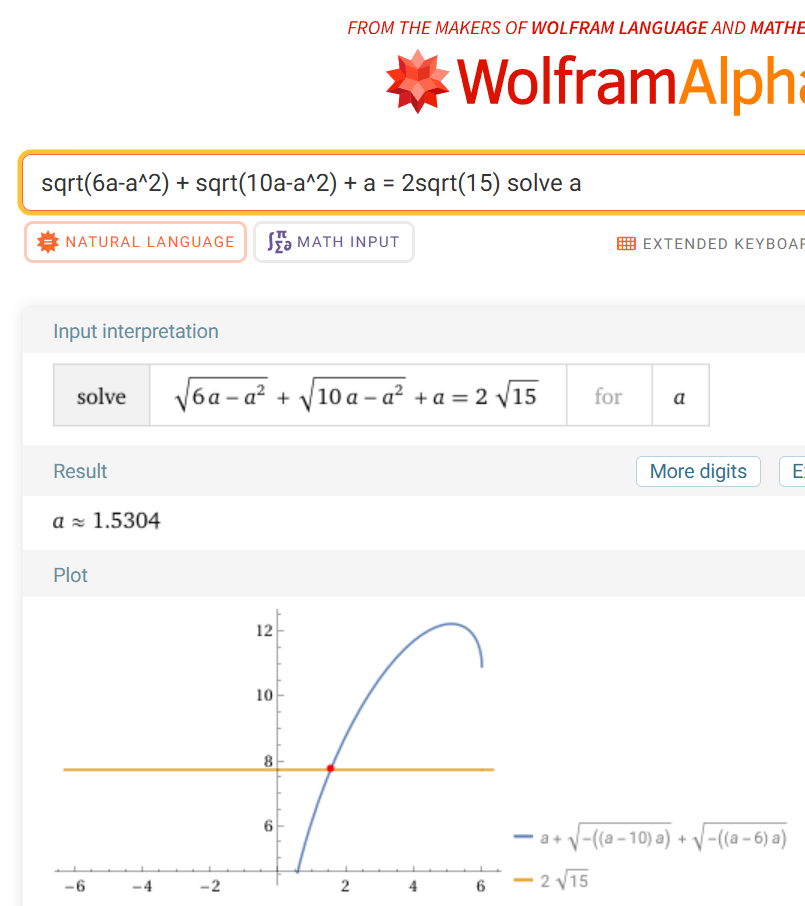
да, через систему 4 уравнений в целом логичнее, но в школе наверное так не будут, скорее всего геометрически будут.
Если хордами, то при радиусах r=3 и R=5 полухорды, лежащие на стороне искомого квадрата имеют длинны x и y, т.е. имеем прямоугольник со сторонами (3-a) и (x+y+a)=2*sqrt(15)
x=sqrt(r^2-(3-a)^2)=sqrt(9-(3-a)^2),
y=sqrt(R^2-(3-a)^2)=sqrt(25-(3-a)^2)
Методов много, надо только определиться, каким требуется решать
+0–
ответить
Это сейчас так изысканно просят помочь с домашкой?? Мол, слабо вам посчитать??
+1–
ответить
Garda Lake ★➦МАЩ• 03.10.25 21:20
Нет. Мне не слабо. Могу посчитать, я в принципе, этим много лет и занималась. Но если для кого-то, то я за это деньги беру. Это называется репитиции
+0–
ответить
Расстояние между нижними точками окружностей 2•✓15, потом с помощью прямоугольных трапеций выражаем через а горизонтальные отрезки за квадратом, суммируем их, добавляем а, и приравниваем к 2♪√15, решаем уравнение. Был бы за компом, расписал бы. Уровень - геометрия 8 класса.
+2–
ответить