История №1262388
О как! Зацепило то многих!
90% тутошних и незамечают как трясут на сайте своим CV ежедневно. Под этим анекдотом особенно наглядно.
Ленка пенка ★➦Pax Slavica• 05.11.21 22:26🇷🇺
У меня есть друг, который рассказал мне эту историю очень давно, и слышал ее как раз от знакомых из Гарварда. Они написали резюме за Перельмана, насколько я поняла :)
Pax Slavica➦Ленка пенка• 05.11.21 22:29🇺🇸
Мой знакомый из гарварда сказал что тоже читал но там поминался Стенфорд :). Вообще Универы очень разделены пофакультетно. Даже по кафедрам иногда. Не понять где какой процесс. Один для постдоков, другой для профессоров. Для персонала так вообще.
Ленка пенка ★➦Pax Slavica• 05.11.21 22:54🇷🇺
Да, может, Стэнфорд. Я сейчас уже не помню. Историю помню.
AK ★➦Ленка пенка• 06.11.21 02:08🇨🇦
Это потому, что он неженатый. Моё резюме писала жена. Я до сих пор его целиком не прочёл. Только позиции добавляю.
Ленка пенка ★➦AK• 06.11.21 02:25🇷🇺
Вот он, гнет мачизма! Я первому мужу тоже писала резюме. Второй как-то без меня долго справлялся, но потом тоже все к этому пришло... ну, пункты добавляла, но много приходилось!
vvt251 ★➦Ленка пенка• 06.11.21 03:43🇺🇸
Это нормально, когда резюме за тебя пишут.
Я тут (на ан.ру) одному человеку писал.
А вот писать про себя,какой я хороший - это противоестественно.
Ленка пенка ★➦vvt251• 06.11.21 05:46🇷🇺
Что верно, то верно. Я когда пишу, всегда представляю, что это не себе.
AK ★• 05.11.21 15:48🇨🇦
Он прав. На это есть агенты по трудоустройству, лоторые получают за это бабки.
Я не Перельман, но даже моё резюме они подгоняют под позицию.
Все-таки тридевятая школа и рукшинские кружки очень сильно на психику влияют...
mathematicus ★➦evengerova• 05.11.21 15:25🇬🇧
Вы знакомы с Григорием Перельманом лично, или это синтетическое априорное суждение?
evengerova➦mathematicus• 05.11.21 17:43🇷🇺
Я знакома лично с большим количеством людей разного возраста из тридевятой школы и рукшинских кружков - симптомы очень похожи. Так же знаю методики обучения 239. Своему ребенку я бы такого точно не пожелала. Народ из других ведущих матшкол Питера - тридцатки, сорок пятого интерната и ЮМШ куда адекватней. А эти дети, измученные усилиями не спуститься в общедоступных общешкольных рейтингах и жесткой конкуренцией, действительно очень болезненно воспринимают любое сомнение в их величии.
mathematicus ★➦evengerova• 05.11.21 21:37🇬🇧
Веничка Ерофеев описывал смерть человека от чрезмерной склонности к обобщениям. В данном случае вы оцениваете ситуацию строго антиномично. Григорию Перельману совершенно неинтересно его так называемое величие. Его гораздо больше беспокоят справедливость и целесообразность. Я помню, мне никак не удавалось это объяснить Маше Гессен, когда та взялась за его биографию. Классический пример тотального расхождения культурных кодов.
Ленка пенка ★➦evengerova• 05.11.21 22:08🇷🇺
Перельман совершенно не страдает манией величия. Как и многие другие выпускники 239-й школы и даже этого самого кружка не к ночи будь помянутого руководителя (теперь ведут-то кружки, кстати, другие люди). Дураки, конечно, есть везде, в том числе среди выпускников любых матшкол. Но это другой случай. Он просто нон-конформист и искренне не приемлет и не понимает бессмыслицы и всякой суеты. Есть особенности характера. Он излишне требователен к себе.
Могу сказать, что я тоже знакома (в огромном количестве) с разными выпускниками и учениками перечисленных Вами школ (забыли ФТШ, кстати, и в оно время 366-ю), и никаких особенных различий между ними не вижу. И там, и там есть хорошие люди и не очень, умные и не очень. Сейчас в 239-й, конечно, временами, так скажем, жгут напалмом, но много есть хороших учителей и хороших учеников.
Ленка пенка ★➦mathematicus• 05.11.21 22:21🇷🇺
От сочинений Маши Гессен о математиках вообще трясет не по-детски. Это ж надо было такому человеку взяться за такую тему! Она же образец бульварщины, прямо хоть в музей. Я как-то почитала чуть-чуть то, что она про Перельмана и других писала, и решила, БОЛЬШЕ - НЕТ. И не стала читать больше.
mathematicus ★➦Ленка пенка• 06.11.21 00:14🇬🇧
Это не бульварщина, это - другое. Ну, вот как вам объяснить... Она с грудным младенцем в декабрьский мороз бегала на Болотную. Чтоб Сеня с первых моментов маленькой жизни проникся борьбой, понимаете? Это - Древний Рим, Горации-Куриации и прочие Гракхи. И сама Маша - это Vir Virtous и Pater Familia. Рядом с ней чувствуешь себя древним германцем: огромное уважение и желание смести всё это большим железным топором. И сочинять эллегии на развалинах.
Ленка пенка ★➦mathematicus• 06.11.21 00:46🇷🇺
Я неправильно написала. Саму Машу я не знаю (хотя, на мой взгляд, таскать младенцев на демонстрации, которые могут окончиться не пойми где - опасная глупость, а таскать младенцев на безопасные демонстрации имеет смысл только с целью прогулки). А вот то, что она пишет, мне кажется редкой бульварщиной. И как она описывает тех людей, которых я знаю... это вообще извращение какое-то, все с ног на голову. Но я прочла очень немного, решила, что не буду умножать скорбь. Я даже думаю, что она не нарочно так, а искренне все это пишет. Но она же вообще в этом ничего не понимает. У нее, видимо, совершенно другое мышление.
Я прошу прощения, что нелицеприятно высказалась про творения человека, которого Вы цените. Возможно, не надо было это писать. Но просто для меня (да и для всех моих друзей-математиков, которые еще лучше знают описываемый ею мир) это что-то запредельное.
mathematicus ★➦Ленка пенка• 06.11.21 01:51🇬🇧
Вы не поняли. Я её глубоко уважаю как человека. И очень ценю как американского писателя. Она - мастер американских лозунгов: "да" - это "да", а "нет" - это "нет", без полутонов. Наука, суть которой - сомнение, и в которой нет места эпической битве бобра с козлом, далека от неё настолько же, как от какого-нибудь Марцелла, которого в завоеванных Сиракузах интересовало только одно: как скоро ученики свежезарезанного Архимеда могут построить ему боевые машины. Она - не просто большевик, она - крестоносец. Для неё истина не просто партийна, для неё враг её врага - априори свят, как союзник по священной борьбе. Все, что она смогла понять про учёных - это, что они решают задачи. Как на олимпиаде. И кто наберёт больше очков - тот самый крутой. Наука - это такой спорт, а Перельман обиделся на нечестное судейство, приписавшее его очки другим. Это "Властелин колец" в переводе Гоблина.
Ленка пенка ★➦mathematicus• 06.11.21 02:15🇷🇺
Такое мировоззрение и литературный стиль очень далеки от созвучных мне, если выражаться толерантно. Я поняла, что это колоритная личность. Жаль только, что она выбрала неподходящую тему, внутренне ей очень далекую. Ну вот представьте себе колоритную личность другого плана, допустим, поэтического настроя девушку, монашку, естественной темой для разговоров которой является духовная музыка и то, не противоречит ли учение о Софии постулату троичности. И вдруг эта монашка решает написать очерк о жизни рэперов и быте сексменьшинств. Или представьте типичную тетку с Привоза, трактующую классическую музыку. Все это колоритные личности, которые могут вызывать симпатию, но вряд ли бы у них получилось что-то не абсурдное - "не садися не в свои сани".
AK ★➦evengerova• 06.11.21 03:59🇨🇦
Достаточно забавно читать о различиях выпускников 30-ки и 239 -ой через сорок лет после выпуска. Впрочем во всём виноваты Рукшин и Братусь Т.А.
mathematicus ★➦Ленка пенка• 06.11.21 04:08🇬🇧
Чтобы сесть не в свои сани, нужна не только самоуверенность, но и определённая отвага. С чем бы это сравнить? С авантюрой Фоменко и Носовского? С приключениями Поля Дирака на ниве математики?
Ленка пенка ★➦mathematicus• 06.11.21 05:47🇷🇺
Ладно. Если я увижу Машу Гессен, я ей обязательно спою. Это будет достойный ответ. К тому же я люблю петь, как и она - писать!
Максим Камерер ★★★★★➦mathematicus• 06.11.21 09:13🇷🇺
Рядом с такими чувствуешь что кто то рядом пропускает прием галаперидолу. Я хорошо знаком с этой вечно-протестной семитской шоблой. Общался накоротке. Общее ощущение: крайняя бытовая эээ неустроенность. Грязь, попросту говоря. Живут они в таких свинарниках, что даже меня, к сквотам привычного, выворачивает от тамошнего амбрэ. С одной такой хаты меня и попросили уйти и не возвращаться. На вопрос: «как ты собралась наводить порядок в России если у тебя в башке и хате такой бардак?»
По молодости я этих дур еб.
Сейчас-брезгую
Максим Камерер ★★★★★➦mathematicus• 06.11.21 09:16🇷🇺
Хорошее описание феерической дуры, не понимающей, что жизнь состоит из полутонов.
evengerova➦Ленка пенка• 06.11.21 15:07🇷🇺
Я не говорила про манию величия, скорее про обостренное чувство самоуважения. И про то, что они дураки не говорила. Они реально крутые, но стиль их общения очень специфический. Согласитесь, странно требовать от секретаря, который тупо следует процедуре трудоустройства и не имеет математического образования, ждать, что он обязан быть в курсе заслуг и работ кандидата.
evengerova➦AK• 06.11.21 15:12🇷🇺
После Вашего выпуска, в смысле? Я-то с ними всю жизнь сталкивалась - в школьные годы в ЮМШ, на мат-мехе как студентка, на мат-мехе как научрук, на работе (у нас большинство с мат-меха и ПМ-ПУ) - мы постоянно студентов берем. Типажи очень характерные :)
evengerova➦mathematicus• 06.11.21 15:30🇷🇺
Безусловно, все люди разные. На кого-то система воспитания влияет сильно, на кого-то не влияет вообще.
Но сам феномен отрицать нельзя - если в школе есть определенные методики, традиции, культура (не важно, хороши они или плохи) - большинство выпускников этой шкулы будут иметь что-то общее. Возможно, к Перельману это не относится. Я действительно с ним лично не знакома, и могу судить только по байкам знакомых и репортажам СМИ.
По поводу целесообразности и справедливости. Есть учреждения, в которых есть процессы (трудоустройства, оплаты, отпусков, etc.) Маленькие учреждения могут существовать и без них, большие - никак. Кто-то эти процессы должен обслуживать. На мой взгляд, целесообразно, чтобы эти процессы обслуживали не крутые математики (которые знакомы с работами Перельмана), а старательные и аккуратные клерки со средним специальным образованием, готовые заниматься однообразной работой. Я не думаю, что ожидание Перельмана, что лично для него сделают исключение из процесса, справедливо (не говоря уже о целесообразности).
AK ★➦evengerova• 06.11.21 15:42🇨🇦
Разговор о Перельмане, правда? Он, кажется, 1964 года рождения...
Я выпускник, как-раз 30-ки.
mathematicus ★➦Максим Камерер• 06.11.21 16:25🇬🇧
Рядом с такими чувствуешь что кто то рядом пропускает прием галаперидолу...
Живут они в таких свинарниках, что даже меня, к сквотам привычного, выворачивает от тамошнего амбрэ.
Полностью мимо. Болезненная чистюля и редкое ощущение душевного здоровья и надежности. Кроме того, фейерическая работоспособность и лояльность к сотрудникам. Я ж говорю, vir virtuous и pater familia. Ей бы эскадроном у Махно командовать. А лучше - кавалерийской алой у Марка Аврелия. "Чтоб жаворонок сказал правду?! правда - одна, и она - воробьиная!"
Гвозди бы делать из этих людей - больше бы было в продаже гвоздей.
Ленка пенка ★➦evengerova• 06.11.21 17:57🇷🇺
Насколько я могу судить, Перельман человек необычный не только потому, что гениальный. Мы в нашей повседневной жизни делаем массу вещей, которые сами же считаем бессмысленными и отчасти ложными, потому что так принято или так надо, жизнь так устроена и т.д. Мне кажется, что он просто не понимает этого совершенно искренне и отторгает на очень глубинном уровне. Ну как человек с абсолютным слухом не может фальшиво спеть "Катюшу", даже если ему объясняют, что здесь принято фальшивить, и вот в этом месте все врут. Он всегда говорит правду. У него, видимо, есть какой-то внутренний камертон, настроенный на простоту и смысл. Ему, думаю, так очень трудно жить, но иначе он, по-видимому, не может. Это, думаю, не сознательное решение, точно не попытка как-то себя поставить, а просто такая врожденная особенность.
Я могла бы сказать, что я знаю Перельмана, в том смысле, что я его, бывало, видела и иногда здоровалась. Но я уверена, что он меня не знает и не помнит абсолютно, поэтому это знакомство односторонне :) Может, самонадеянно так говорить, но нередко у меня о человеке складывается правильное первое впечатление, просто по лицу. И если бы мне сказали пофантазировать и предположить, что это за человек, то я бы сказала, что это человек, лишенный честолюбия и даже обычной доли самолюбия, крайне требовательно относящийся к себе, которому горько, что мир несовершенен, и от этого или еще чего-то он замыкается в себе, и радости которого находятся в, так скажем, области высших частот (красота математики и музыки). Безусловно, это отсебятина. Но "обостренное самоуважение" там точно и не ночевало, он не такой, как те, о ком Вы думаете, он вообще не похож на большинство людей.
Ленка пенка ★➦evengerova• 06.11.21 18:01🇷🇺
Да разные есть люди. Я сама и мои друзья учились в разных ФМШ, занимались в маткружках, в том числе во Дворце. Многие из моих друзей получали золотые медали на международных олимпиадах по математике. (Увы, мне это как-то не передалось диффузией... :) У нас совершенно нормальный стиль общения. Одна моя подруга, которая превосходит меня во всем - красоте, уме, таланте, карьере и др. - вообще безумно застенчива и не может ни обидеть мухи, ни отказать коллегам в помощи.
evengerova➦Ленка пенка• 06.11.21 18:21🇷🇺
Походу, у нас должно быть много общих знакомых. Марину Маслову, Мишу Кшевецкого или Костика Ушакова не знаете, случайно?
Ленка пенка ★➦evengerova• 06.11.21 18:24🇷🇺
Может, я их видела когда-то, но не узнаю. Я могла бы назвать других вероятных общих знакомых, но я ужасно шифруюсь, так как здесь я такого наговорила, что лучше мне личико не открывать! Кто Вы, я поняла (прошу прощения за отсутствие взаимности), могу только сообщить о своем уважении.
evengerova➦Ленка пенка• 06.11.21 18:32🇷🇺
OK. Кстати, если вдруг будете искать работу - стучитесь в ВК :)
Ленка пенка ★➦evengerova• 06.11.21 19:54🇷🇺
Спасибо! Пока я и в РАН, и преподаю, и дипломники у меня, и ничего не успеваю. Но мало ли что!
sasha22148➦Максим Камерер• 09.12.21 05:11🇷🇺
ну, опыт- сын ошибок. как то так. ничего плохого.
sasha22148➦evengerova• 09.12.21 05:14🇷🇺
не странно.
хороший секретарь-на вес золота.
пример-Донна из сериала-Форс-мажоры.
очень рекомендую посмотреть данный сериал. это шедерв.
опять же, команда делает капитана.
Pivo Vodkin ★• 05.11.21 14:14🇷🇺
Девочка ХР-манагер, производящая начальный отсев кандидатов, может и не знать его работ.
"Ты хотя и гениальный, но порядок быть должон!"
Будь ты хоть Чагин, Фирдоусов или Кабиров, но встречному гайцу права покажи, чтобы он убедился, что ты отучился в автошколе и сдал экзамен.
irrazionalle➦Pivo Vodkin• 05.11.21 14:36🇷🇺
У некоторых гонщиков топ уровня в начале выступлений прав на управление гражданской машиной не было. У Смоляра и сейчас нет. Он, правда, пока не топ.
Lokk➦Pivo Vodkin• 05.11.21 15:05🇪🇸
Давно как-то попадалась история о водителе в Великобритании, в 1980-х +/-, которого полиция остановила на проверку документов и выяснилось что прав нет и не было, т.к. водить он начал до введения ВУ в 1934 г. Отпустили.
robin1➦irrazionalle• 05.11.21 22:56🇷🇺
так и пускай гоняет по спецтрассе! а дороги общего пользования, это для обученных, с правами
Редиска➦Pivo Vodkin• 06.11.21 05:37🇨🇦
Если его попросили прислать резюме, то начальный отсев он уже прошел.
И вообще, наличие ученых такого уровня в штате университета значительно влияет на рейтинг и престиж университета. Поэтому за таких ученых есть конкурентная борьба. Так что это не тот случай.
Pivo Vodkin ★➦irrazionalle• 06.11.21 12:33🇷🇺
Стасиса Бурундзу из какой-то прибалтийской ССР (не помню, какой именно из трёх) в родной республике гайцы не штрафовали за превышения скорости. Потому что понимали: человек знает, что делает, и если едет с этой скоростью, значит, для него она безопасная.
Интересно, когда Эйнштейна принимали на работу в Принстон, местные чинуши тоже заставили его писать резюме и бегать по собеседованиям?
ПионЭры➦Plato• 05.11.21 15:14🇷🇺
показать комментарийКто-то ещё считает Эйнштейна гениальным ученым?
Dimas ★➦ПионЭры• 05.11.21 15:43🇩🇪
Частично соглашусь . Среди населения земли доля бесконечно дремучих созданий, считающих себя человеком, стремительно растет. Они , разумеется, не считают Эйнштейна гениальным учёным.
Пионэр, если бы только краем уха слышал, за что Эйнштейну Нобелевскую дали...
Проффессор ★➦ПионЭры• 05.11.21 16:40🇺🇸
А что, достаточно посмотреть ютюбовских дешёвок, сляпанных на уровне кликбейта, чтобы убедиться в обратном? Может стоит почитать хотя бы одну монографию Эйнштейна в оригинале прежде, чем утверждать такую несусветную чушь?
Michael Ashnin ★★★➦Проффессор• 05.11.21 16:55🇺🇸
Ты прав…
Там этих псевдонаучных отмороженных дегенератов — пруд пруди!!
ystervark➦Проффессор• 05.11.21 17:34🇿🇦
а почему обязательно в оригинале? Это же не художественный текст и даже не философский, в переводе ничего не теряет. И о какой монографии речь? Он же статьи писал, короткие. Я читал парочку. Правда, не те, за которые нобелевку.
Randajad ★➦ПионЭры• 05.11.21 20:03🇮🇱
Странно, очень странно. Был такой физик, тоже Нобелевский лауреат, звали его Ричард Фейнман. Так вот, он в своей книге "Вы, конечно, шутите, мистер Фейнман!" очень высоко и с трепетом отзывался об А. Эйнштейне. Но кто такой этот Фейнман, кто его знает, разве, что недоумки, типа меня. Я, например, очень ценил его цикл лекций "Фейнмановские лекции по физике", с удовольствием изучал их.
Pax Slavica➦Dimas• 05.11.21 21:06🇺🇸
За фотоэффект дали Нобелевскую, но это не касается 99% жилеткой земли. Слышали про него решительно все.
ManBearPig➦Pax Slavica• 05.11.21 21:28🇳🇴
Жаль, что так низко пало образование, что ты не знаешь за что дали Нобелевскую премию Эйнштейну
Randajad ★➦ManBearPig• 05.11.21 21:41🇮🇱
А что, собственно, неправильно. Эйнштейн номинально получил нобелевку в 1922 году за открытие закона фотоэлектрического эффекта и другие работы в области теоретической физики. Хотя его начали выдыигать ещё с 1910 года.
В 1973 году, на моё тринадцатилетие родители подарили книгу "Эволюция физики" Эйтштейна. Она у меня хранится до сих пор.
Pax Slavica➦ManBearPig• 05.11.21 22:00🇺🇸
Жаль что вас так и не воспитали ни родители ни общество не говорить незнакомым людям ты.
Если память подводит, пользуйтесь Википедией. 1921 год. Фотоэлектрический эффект.
Pax Slavica➦Randajad• 05.11.21 22:02🇺🇸
99% считают что за СТО дали, так как это самая популярная работа.
Ну и то что СТО это уточнение ТО Пуанкарэ, тоже редкое знание. Но так ли оно обязательно?
Randajad ★➦Pax Slavica• 05.11.21 22:13🇮🇱
Насколько я помню, на нобелевку за создание специальной теории относительности Эйнштейна выдвигали ещё в 1910 году. Но тогда нобелевский комитет посчитал, что многое не доказано и слишком "революционно". Насчёт теории относительности Пуанкаре, "так, тилькы трошечки нэ так". Пуанкаре использовал теорию эфира, в тоже время Эйнштейн отказался от этой теории. Хотя оба использовали преобразования Лоренца. Есть достаточно много отличий, можно об этом говорить долго, но не на этом форуме.))
Pax Slavica➦Randajad• 05.11.21 22:22🇺🇸
И на этом форуме бывают люди которые Пуанкаре не только из-за Понтрягина (Перельмана) помнящие :)
Randajad ★➦Pax Slavica• 05.11.21 22:25🇮🇱
Тем более будьте снисходительны. Иначе обсуждение истории превратится в обсуждение какой-либо проблемы из области математики или физики. Потом пойдут в ход теоретические выкладки и пошло поехало.)))
Pax Slavica➦Randajad• 05.11.21 22:26🇺🇸
Я бесконечно далёк от теории непрерывных групп.
«Книжка у препода лежала на столе, запомнил просто по приколу» :D
Pax Slavica➦Randajad• 05.11.21 22:27🇺🇸
Разве что вы заслушаете метод Баума-Уэлша для скрытых Марковских моделей.
Randajad ★➦Pax Slavica• 05.11.21 22:29🇮🇱
Так и я - радиофизик. Вообще, последние 20 лет занимаюсь проблемами видео аналитики в системах видеонаблюдения. А всю общую физику, включая теорию относительности, помню только из курса университета.
Randajad ★➦Pax Slavica• 05.11.21 22:34🇮🇱
Алгоритм Баума - Уэлша, как вероятностная модель множества случайных переменных - это очень интересная тема на anekdot.ru, но может поговорим о чём-нибудь весёлом, например, "что слышно о холере в Одессе". )))
Pax Slavica➦Randajad• 05.11.21 22:42🇺🇸
Есть ли место нейрометрия в видео аналитике?
А то фотки уже школьники анализируют на «котик» или «собачка».
Тёр веру место в жизни есть :)
Pax Slavica➦Randajad• 05.11.21 22:44🇺🇸
Да ладно в Одессе, графстве Кент (штат Огайо), такое творится, такое. Все пьют витамины и покупают (не скажу что) из под полы. Святая демократическая инквизиция дремлет!
Randajad ★➦Pax Slavica• 05.11.21 22:45🇮🇱
Вы, как мне кажется, на грудь принять изволили, по поводу окончания рабочей недели.))
Pax Slavica➦Randajad• 05.11.21 22:48🇺🇸
Я только лично вам могу сказать за графство Кент и не на этом форуме. Но информация интересная.
Я на медикаментах. Выпивать нельзя.
Randajad ★➦Pax Slavica• 05.11.21 22:50🇮🇱
Верю, когда-то в прошлом, вернее в позапрошлом веке, некоторые, запрещённые сейчас вещества тоже считались медикаментами.))
Pax Slavica➦Randajad• 05.11.21 22:56🇺🇸
Были такие. От поноса и от кашля :).
А сейчас даже лидокаин только животным. А уж про средство от паразитов… люди покупают «для лошади».
Randajad ★➦Pax Slavica• 05.11.21 22:59🇮🇱
Ага, а кокаин почти до 20-х годов прошлого столетия применяли, как капли от насморка.)))
Pax Slavica➦Randajad• 05.11.21 23:01🇺🇸
Китай так тот до конца 1960х боролся с наследием опиумных войн.
ПионЭры➦Dimas• 06.11.21 00:18🇷🇺
Неужели за Теорию Вероятности? Нет?
А за что?
Фотоэффект?
Эйнштейн его открыл или изобрёл? тоже нет?
А что он сделал с Нобелевской премией, знаешь? А почему, знаешь?
А много ли научных работ у Эйнштейна без соавторов? Когда он стал известным ученым...
Dimas ★➦Pax Slavica• 06.11.21 00:20🇩🇪
Фотоэффект может быть не касается некоторого количества людей на Земле. В самых-самых малоразвитых уголках, но сложно найти хоть какую-то область приложения человеческих усилий , где фотоэффект хоть как-то не используется .
ПионЭры➦ПионЭры• 06.11.21 00:21🇷🇺
Теорию Вероятности путаешь с Теорией Относительности?
Сейчас последний осёл ткнёт мордой жеж!
Pax Slavica➦Dimas• 06.11.21 01:05🇺🇸
Фотоэлектрический эффект. Не уверен что знаю о чем это. Может и не относиться к фотографии
vvt251 ★➦Randajad• 06.11.21 03:51🇺🇸
// Хотя оба использовали преобразования Лоренца. //
Вообще-то, Пуанкаре и вывел преобразование Лоренца и он же его преобразованием Лоренца и назвал (идея была Лоренца, но у него математики не хватало, чтобы вывести).
Но теорию относительности сделал Эйнштейн, а до него это только набор формул был (правильных), но никто не понимал что это значит.
Randajad ★➦vvt251• 06.11.21 10:49🇮🇱
так я не спорю. Всё, что касается теории относительности я последний раз сталкивался в университете этак более тридцати пяти лет назад.
sasha22148➦Randajad• 09.12.21 05:34🇷🇺
я слышал про такого. все хочу почитать эту его книгу. да все руки не доходят.
Некто Леша ★★★★★• 05.11.21 12:57🇷🇺
Под Камерера эту историю можно перелицевать так:
90-е. Подцепил в клубе милую барышню, с обликом невинной овечки. Заехал на остаток ночи с ней в сауну, оказалось - ненасытная гурия любви и большая искусница в этом деле. К утру чувствовал себя как выжатый лимон, но с ней хотелось выжимать этот лимон снова и снова, без отрыва от работы - созрел лимон, пусть выжимает, лишь бы была под рукой. Спросил расставаясь, где живет и работает, оказалось - у чертей на куличках, чуть ли не в Бирюлево, секретаршей у какого-то престарелого мудака, который ебет ее лишь раз в день. Такой талант пропадает! Предложил устроить ее на работу к себе поближе, к кому-нибудь из знакомых, попросил прислать резюме. Она отвечает:
- Да я с половиной Москвы переспала, за вычетом нищебродов конечно. Если они знают, как я трахаюсь, то им не нужно мое резюме. А если им нужно мое резюме, значит они ничего не знают о том, как я трахаюсь, и не возьмут меня секретаршей за 30 тысяч баксов в месяц!
mathematicus ★➦Некто Леша• 05.11.21 15:19🇬🇧
Хотел бы я посмотреть соответствующее резюме. С сертификатами, рекомендациями с мест имения и проч.
Хм, тянет на сценарий хорошего порнофильма с латинским названием Curriculum Vitae (описание жизни, также
резюме).
mathematicus ★➦Kelavrik_0• 05.11.21 15:15🇬🇧
Ну, и не быть им вместе - Перельману и Гарварду.
Pax Slavica➦Kelavrik_0• 05.11.21 21:02🇺🇸
Чиновники ответственны за формальную сторону. По существу вопрос решает кафедра.
Kelavrik_0➦Pax Slavica• 05.11.21 22:30🇷🇺
Ну так к формальной стороне относится и список достижений.
Pax Slavica➦Kelavrik_0• 05.11.21 22:47🇺🇸
Так то да. Процесс рассмотрения может начинаться с формальной стороны, типа «у кого нет резюме тех вон».
Следующий этап, думаю, это есть ли опечатки в резюме. А там ещё и «research statement» может требоваться.
Но как говорит Ленка в одном из комментов, видимо Перельмана заметили и пошли на встречу.
Kelavrik_0➦Pax Slavica• 05.11.21 23:15🇷🇺
Ну да, просто у нас все крутые спецы давно освоили бюрократическую сторону вопроса и она не вызывает удивления.
Хренонимус ★• 05.11.21 12:25🇱🇻
Так-то оно так, но академики народ обидчивый (сам видишь) - забудешь в его резюме (а указания регалий требуется в акад.среде, чтобы тебя приняли официально) указать его малоизвестную, но важную для него, публикацию, обид будет до небес ;)
"Чем ближе к докторской - тем дальше в детство" у моих подопечных такая поговорка ходит.
Gang➦Хренонимус• 05.11.21 12:51🇨🇿
Его резюме пишет он сам. Или не пишет. Как в нем может ошибиться кто-то другой?
Pivo Vodkin ★➦Gang• 05.11.21 14:19🇷🇺
Ну почему же, вполне может написать секретарь или другие лица... Мало ли какие, несомненно, очень уважительные, причины могут помешать академику написать резюме собственноручно.
mathematicus ★➦Хренонимус• 05.11.21 15:14🇬🇧
В отношении Перельмана это особенно верно. О его лучших работах знают разве что пара сотен человек, способных понять аннотацию к ним. (Я к ним, увы, не отношусь.) По их мнению, это гораздо круче доказательства прославленной гипотезы геометризации.
marek➦mathematicus• 05.11.21 16:44🇮🇱
А меня всегда занимал вопрос:
Всё что придумано математиками с некоторым "лагом" используется физиками и/или другими естественно научными дисциплинами.
Я не понимаю чем заняты современные математики (мозгов не хватает). Но может кто-нибудь кто понимает может предсказать как это будет?
Хренонимус ★➦Gang• 05.11.21 17:03🇱🇻
За наших докторов очень часто руководители программ пишут.
Ему присылают (если повезло) список публикаций и где числился и, айда.
Аккедитационной комиссии похрену Перельман у тебя читает лекции, Вассерман или еще кто. Список публикаций и СВ дай.
vvt251 ★➦marek• 05.11.21 17:23🇺🇸
// Всё что придумано математиками с некоторым "лагом" используется физиками //
Не совсем так. Большая часть математики, которую использует физика была либо придумана физиками, либо переоткрыта физиками (так как они этого не знали, а понадобилось). Иногда между математиками и физиками была война на тему как "правильно".
Например, обобщенные функции придумали физики, а математики долго говорили, что таких функций не бывает. Потом сдались, но сказали, что вы все неправильно придумали, надо ... . В итоге физики своими определениями пользуются, математики своими, но иногда, при вычислениях, ответы разные получаются, и тогда между математиком и физиком лучше не стоять - зашибут и не заметят.
irrazionalle➦vvt251• 05.11.21 18:21🇷🇺
Математика — это язык, на котором написана книга природы (с) Г. Галилей
Видимо разные диалекты используют физики и математики. Но и те и другие, определенно, ученые.
Как мне тут один забавный персонаж утверждал, что местоимение Вы нужно писать обязательно с большой буквы, когда к нему обращаешься )
Пустое вы сердечным ты
Она, обмолвясь, заменила
И все счастливые мечты
В душе влюблённой возбудила.
Пред ней задумчиво стою,
Свести очей с неё нет силы;
И говорю ей: как вы милы!
И мыслю: как тебя люблю!
А.С. Пушкин
marek➦vvt251• 05.11.21 18:37🇮🇱
Спасибо.
На моем мизерном уровне понимания математики -- лучший пример это комплексные числа и электротехника.
Ну или Булева алгебра и компы.
И очень бы хотелось чтобы кто-то понимающий математику на осове её сегодняшней сказал бы "что там впереди".
marek➦irrazionalle• 05.11.21 18:40🇮🇱
Математика — это язык, на котором написана книга природы
Я всегда думал что это Ньютон.
Вот и хочется чтобы знающий этот язык заглянул на пару страниц вперед
irrazionalle➦marek• 05.11.21 18:53🇷🇺
Знание языка не означает наличия ясновидения.
В 2000 году распивая спиртные напитки в компании возник вопрос. Процессоры уперлись в частоту 3Гц и вроде дальше было никак. Соответственно - что дальше?
У меня возникло предположение, что это не проблема. Есть же сервера с двумя CPU. Просто возьмут и сделают матплаты на 4,8,16,23 CPU. Если техпроцесс позволит, то уменьшится площадь самого кристалла. И можно будет докупать юниты по мере необходимости, а те, что не используются будут закрыты заглушками.
Но практика показала, что многопоточность и многоядерность это правильный путь, а вот его реализация отличается от предположения.
Некто Леша ★★★★★➦marek• 05.11.21 18:58🇷🇺
Разговорился я как-то на фуршете с одним математиком в Куала-Лумпур, скромным выпускником тамошней магистерской программы, лет 25.
Оказалось, он математик по базовому образованию на уровне бакалавриата, но в качестве основателя и владельца сингапурской компании почувствовал однажды, что именно этой малазийской магистерской программы ему не хватает для дальнейшего развития его бизнеса, и формат обучения удобный - надо прилетать из Сингапура в Куала-Лумпур только два раза в семестр.
Первый раз в начале семестра, для слушания установочных лекций, нетворкинга и заражения общей атмосферой, как охрененно то, что им собираются преподавать, трип дня на три.
Второй раз - в конце семестра, живые обсуждения его итогов и сдача экзаменов, еще три дня. Все остальное время - обучение по удаленке без отрыва от бизнеса, в любое свободное время.
- А что за бизнес-то, что так можно учиться? - удивился я.
Обработка биг дата записей видеокамер супермаркетов с разработкой эвристических алгоритмов обработки этих данных с целью определить поведенческие реакции покупателей - как они реагировали на раскраску упаковки, на яркие стикеры со скидками, на размер, объем и стиль шрифта надписей, на какие товары повернули голову проходя мимо, какие из конкурирующих товаров задумчиво перебирали на полке, какие оплатили на кассе.
В общем, наука продвинутого рыболова в ситуации, когда на крючок должны попасться не рыбы, а люди. И ни в коем случае не соваться на чужой крючок. Это был 2010. Какие скачки совершила наука математика с тех пор, лучше не думать.
vvt251 ★➦marek• 05.11.21 19:00🇺🇸
Одного известного ученого, в интервью спросили: какие проблемы будет его наука решать через 25 лет.
На что он ответил, что если бы он это знал, то занялся бы этими вопросами сегодня.
Морж➦irrazionalle• 05.11.21 19:04🇺🇸
В школе все правила не дают.
"Вьi" при обращении с большой буквьi вообще факультативно, а после 1-го употребления и вовсе не особо рекомендуется.
marek➦vvt251• 05.11.21 19:52🇮🇱
Спасибо всем. Очень интересно.
Ну переформулируем вопрос так (чтобы не претендовать на ясновиденье и будущие проблемы)
Какие реализации в реальном мире могут в будущем иметь уже решенные сегодня математические задачи?
Интересно по 2м причинам:
Интересно же что будет-то?
Хоть немного понять чем современная математика занимается?
Хренонимус ★➦irrazionalle• 05.11.21 20:04🇱🇻
Эээ, сразу видно х86 человека :))
Солярщики в 2000ых не удивлялись 24 процам :)
Встречайте, Sun Fire (2001г)
https://gcn.com/articles/2001/10/05/sun-launches-72processor-sun-fire-server.aspx?m=1
Randajad ★➦Некто Леша• 05.11.21 20:23🇮🇱
Лёша, на сегодняшний день существуют алгоритмы VA(video analytics), реагирующие на определённые поведенческие реакции человека (группы людей). Я был на семинаре по новым системам CCTV и системам VA. Как раз подымалась тема предсказания поведенческих реакций при определённых условиях.
Gang➦Pivo Vodkin• 05.11.21 20:45🇨🇿
Ну, мне бы в голову не пришло сравнивать Перельмана, без сомнения, гения с ... Мда, на этого намекали с самого начала. А я не понял. Ну, забыл я, что он - академик. Да, а по какой специальности?
А докторскую он тоже защищал?
Математика огромна. Мы не можем знать, какая ее часть будет использована следующей. Более того, новая физика может еще раз использовать уже применявшуюся математику.
Gang➦irrazionalle• 05.11.21 20:50🇨🇿
А в Чешском может быть Вы, вы, Ты и ты. С разными значениями.
Но попробовать-то можно?
Чтоб хоть как-то понять чем математики сейчас заняты#
mathematicus ★➦vvt251• 05.11.21 21:57🇬🇧
Между обобщенными функциями Дирака и Шварца - 20 лет. Не так много, чтобы превратить формальное эвристическое исчисление во внутренне непротиворечивую теорию. Потому что всё это: "рассмотрим функцию, всюду, кроме нуля, равную нулю, в нуле - бесконечность, а общим интегралом - единица", это все равно, что сказать: "возьмём красную фанеру зелёного цвета и покрасим её в прозрачный цвет".
Но вы лучше мне расскажите, как Эйнштейн переоткрывал Гауссиан и Центральную Предельную Теорему. Или модель Пуанкаре. Или как физики переоткрывали алгебры фон Неймана. Или как специалисты по теории очередей переоткрывали цепи Маркова и процесс Пуассона-Хинчина. Я весь одно огромное ухо.
mathematicus ★➦marek• 05.11.21 22:00🇬🇧
Чтоб хоть как-то понять чем математики сейчас заняты
Например, пытаются превратить возможно большее число областей исследования - в вычисляемые. Это общий тренд.
irrazionalle➦Хренонимус• 05.11.21 22:23🇷🇺
Там суть не в количестве, а в принципе. Многопроцессорные суперкомпьютеры уже существовали к тому моменту (Deep Blue например). Смысл идеи в том, что апргрейд делается не сменой платформы целиком, а просто добавлением необходимого количества юнитов. И это могло быть доступно "в гражданском сегменте", к которому, без сомнения, относился x86.
Хренонимус ★➦irrazionalle• 05.11.21 22:40🇱🇻
Ну все еще впереди ;)
Сейчас очередной барьерчик (гейты транзистора уже такие-же как сам транзистор), не одолев который транзисторы нужно будет растить либо в третье измерение (с сопутствующим гемором теплоотведения и коммутации) либо как видеокарты - туева хуча процессоров и ядер.
marek➦mathematicus• 05.11.21 22:48🇮🇱
Например, пытаются превратить возможно большее число областей исследования - в вычисляемые. Это общий тренд.
"Решение всего" численными методами?
Чур тапками не кидать!
vvt251 ★➦mathematicus• 06.11.21 00:32🇺🇸
Во-первых, я не сказал, что все было придумано физиками.
Но, на данный момент есть две науки с сокращением ММФ. Одна методы математической физики, вторая математические методы физики. И это сильно разные науки.
Что было переизобретено физиками? Например, Гейзенберг, для своих нужд в квантовой механике изобрел нечно, что было некоммутативно, .... . Когда он рассказал об этом странном объекте знакомому матетемитику, тот подумав, сказал, что есть такое - называется матрицы.
Что касается обобщенных функция, то я с физическим и математическим описанием их натрахался много. Диплом я делал в конце 70х, мой руководитель был чистый математик (в стекловке работал). И при решении задачи у нас получался разные ответ (при этом я пользовался "физическим" определением обобщенных функций, а он "математическим").
Если упростить то что мы делали (название диплома было "использование объединенной квантово-классической алгебры для ...") то разобраться можно на примере прохождения частицы через потенциальный барьер:
V=0 для x < 0, и V = U0 для x > 0. Решается уравнение Шредингера (уравнение Штурма-Лиувилля второго рода), волновая функция справа и слева сшивается на границе ... - в общем все стандартно, в любом учебнике есть.
Ответ для коэффициэнта отражения от такой ступеньки, в случае если энергия частицы больше чем U0 на картинке.
Проблема в том, что есть теорема, что классический ответ получается из квантового, если взять предел постоянная планка стремитсяс к 0. Но в ответ для коэффициэнта отражения постоянная планка не входит. Значит этот ответ верен как к классическом, так и в квантовом случае. А значит если я брошу мяч, который летит выше крыши дома, то рискую получить им обратно в лоб с вполне конечной вероятностью.
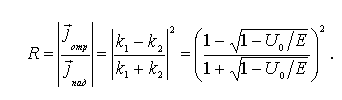
mathematicus ★➦vvt251• 06.11.21 05:20🇬🇧
Я туплю? Это ведь решение уравнения с классическим гамильтонианом, не с квантовым? Дифференциальное уравнение второго порядка, не псевдо-дифференциальное первого? Нет?
vvt251 ★➦mathematicus• 06.11.21 05:35🇺🇸
Это обычное уравнение второго порядка с граничными условиями.
Слева решение exp(i*k1*x)+a*exp (-i*k1*x) справа b*exp (i*k2*x)
При сшивке в 0 функция и производная должны быть неприрывными. Отсюда находятся а и b (k1 и k2 находятся до того из энергии и величины U0).
На самом деле твой вопрос - это общая проблема, мы на разных языках говорим (поэтому и переоткрытия). Я однажды решал такое уравнение, где-то ошибался - ответ был очевидно неправильным. Рассказал знакомому математику. Показал ответ - ожидал, что он подпрыгнет и закричит, что так не бывает (собственное значение уравнения было меньше чем минимум потенциала). На него это не произвело никакого впечатления. А результате, вместо получения советов, я все время потратил на то чтобы объяснить почему собственное значение таким быть не может.
mathematicus ★➦vvt251• 06.11.21 11:06🇬🇧
Минимум собственного значения зависит от граничных условий, грубо говоря. Или от поведения на бесконечности, если интервал неограниченный. Кстати, если интервал неограниченный, то решение, что ты приводишь, не есть ψ-функция, так что собственное значение, что вы нашли, не есть уровень энергии.
Но дело не в этом. Давай вспомним, с чего мы начали обсуждение. Ψ-функция для классического гамильтониана получается из ψ-функции квантового гамильтониана переходом к пределу при постоянной Планка h стремящейся к нулю. Это значит, что решение уравнения Шрёдингера с классическим Гамильтонианом (т.е. задачи Штурма-Лиувилля) и не может зависеть от постоянной Планка - ведь вы уже перешли по ней к пределу.
Disclaimer: все это рассуждение решительно перестаёт работать, если мы говорим, например, о конденсате Бозе-Эйнштейна.
vvt251 ★➦mathematicus• 07.11.21 01:20🇺🇸
Насчет потенциала (разница между физиком и математиком) - потенциал на бесконечности всегда может выйти но 0 (умножу на функцию, которая равна возле 0 единица, а за сто световых лет плавно выходит на 0).
При любых граничных условиях (с учетом регуляризации) минимальное собственное значение всегда больше минимума V(r) (уравнение ниже). На эту тему есть теорема, про которую помнят только те, кто живет на границе математики для физиков и математики для математиков (чистым математиками она не нужна - слишком частный случай, для физиков она тоже не нужна - это и так очевидно).
Теперь про Гамильтониан - он состоит из двух часте (уравнение внизу). Первая часть (лапласиан) - кинетическая энергия - в нее входит постоянная Планка, вторая часть (V(r) ) - потенциальная энергия. Она обычно не содержит постоянную Планка. Так что постояная планка в ответ входит через первый член (которые всегда одинаковый).
Решение выходит на классической, когда постоянная Планка в кинетической энергии стремится к 0.
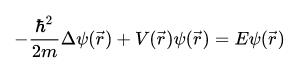
mathematicus ★➦vvt251• 08.11.21 00:28🇬🇧
"Чистые" математики теорему Лакса-Мильграма и прочие квадратичные формы очень уважают.
Потенциал V в уравнении, что вы привели, как я понял, отрицательный? Ну, по меньшей мере, знакопеременный?Иначе я элементарно докажу, что минимальный уровень энергии Е=0. Если, конечно, вы локализовали V на ограниченный объем, и на этом объёме у него слабая сингулярность.
vvt251 ★➦mathematicus• 08.11.21 01:19🇺🇸
Знак потенциала неважен - я всегда к нему положительную константу прибавить могу.
Для простоты пусть будет 0 на бесконечности и где-то отрицательный (а есть ли точки где он положительный - неважно).
Или бесконечный на бесконечности (например a*r^2).
Это все равно. Минимальное собственное значение всегда больше минимума V (оба определены с точностью до константы).
mathematicus ★➦vvt251• 09.11.21 04:48🇬🇧
Если этот потенциал положительный и равен нулю на множестве бесконечной ёмкости, то минимум потенциала - ноль, и дно спектра - тоже ноль. Причём этот ноль не есть собственное значение, потому что достигается не на ψ-функции, а на аппроксимирующей последовательности. При слабой сингулярности спектр вообще не отличается от спектра Лапласиана: непрерывный спектр заполняет положительную полуось.
А вот если потенциал растет, у вашего оператора компактная резольвента и дискретный спектр.
vvt251 ★➦mathematicus• 09.11.21 05:35🇺🇸
В любом случае минимальное собственное значение больше минимума потенциала.
Это верно и для непрерывного спектра и для дискретного.
Но может быть состояния энергия которого меньше минимума потенциала.
mathematicus ★➦vvt251• 10.11.21 15:52🇬🇧
В любом случае минимальное собственное значение больше минимума потенциала.
Строго больше? Что-то я не представляю себе такого. Разве что минимум потенциала отрицательный. Тогда там интегральная норма потенциала появляется.
Но может быть состояния энергия которого меньше минимума потенциала.
Это как? Минимум очень большой!
vvt251 ★➦mathematicus• 13.11.21 02:14🇺🇸
Да, строго больше. Даже в патологическом случае, постоянного потенциала, решение с собственным значеним равным потенциалу будет константой, а значит оно не нормированное.
// Разве что минимум потенциала отрицательный. //
Знак, как я уже говорил - не имеет значения, я всегда могу прибавить константу и все на эту константу сдвинется.
Вообще, если предел потенциала на бесконечности равен V+, на минус бесконечности равен V-, а минимум потенциала Vmin. Необходимым, но недостаточным условием существования дискретного спектра является условие Vmin < min(V+,V-). И дискретный спектр En лежит в интервале Vmin < En <= min(V+,V-).
sasha22148➦Некто Леша• 09.12.21 05:50🇷🇺
мужик. да я окуел просто. много интересных букв. я такое давно не видел. ты -большая редкость.